Magnetic actuation

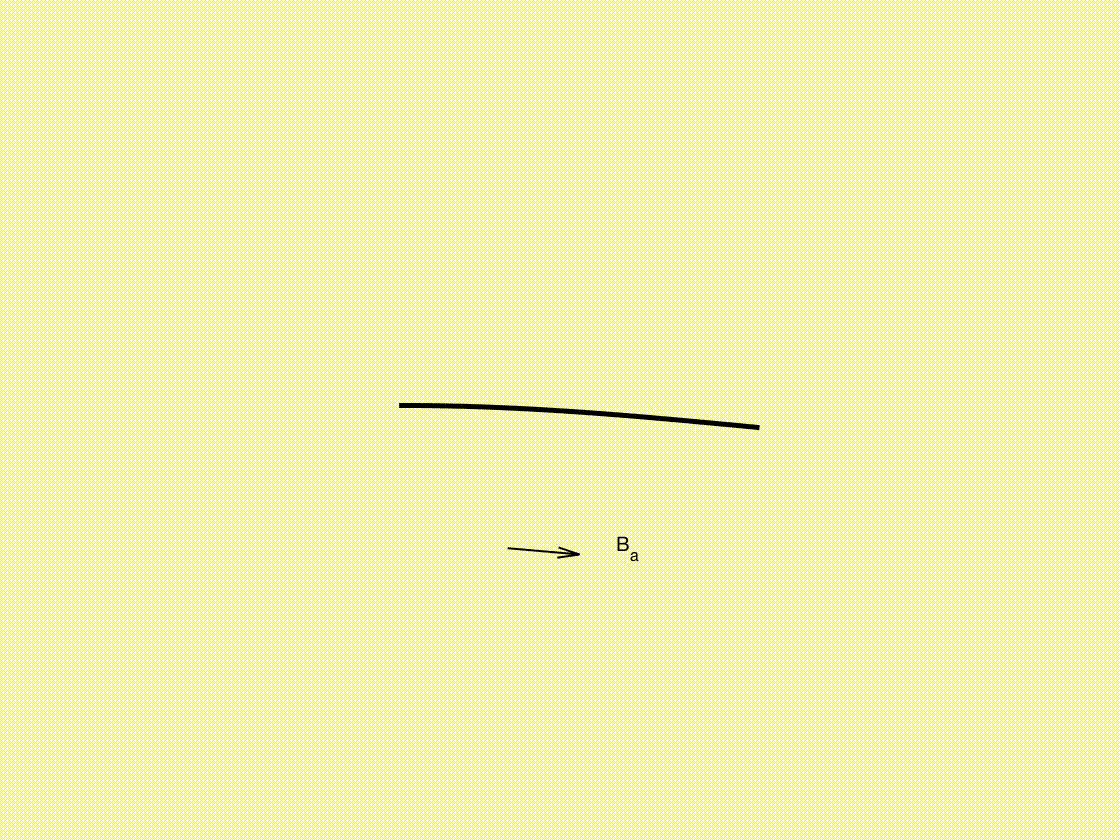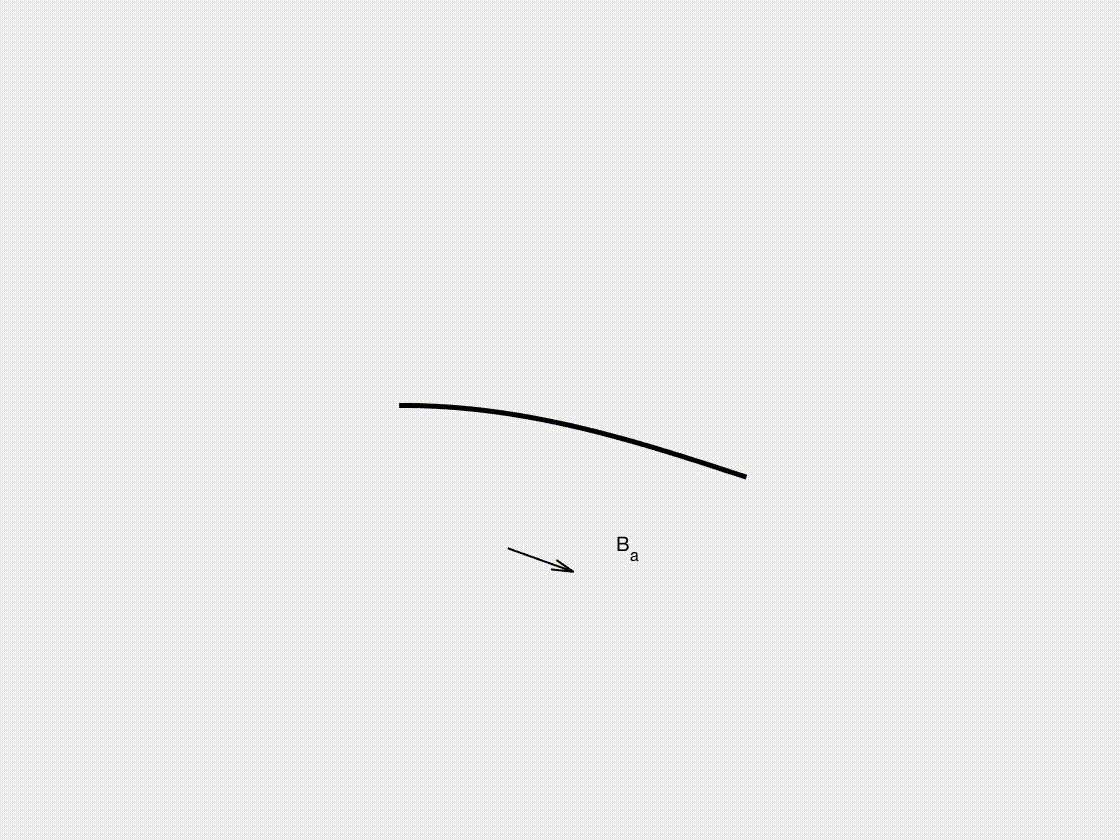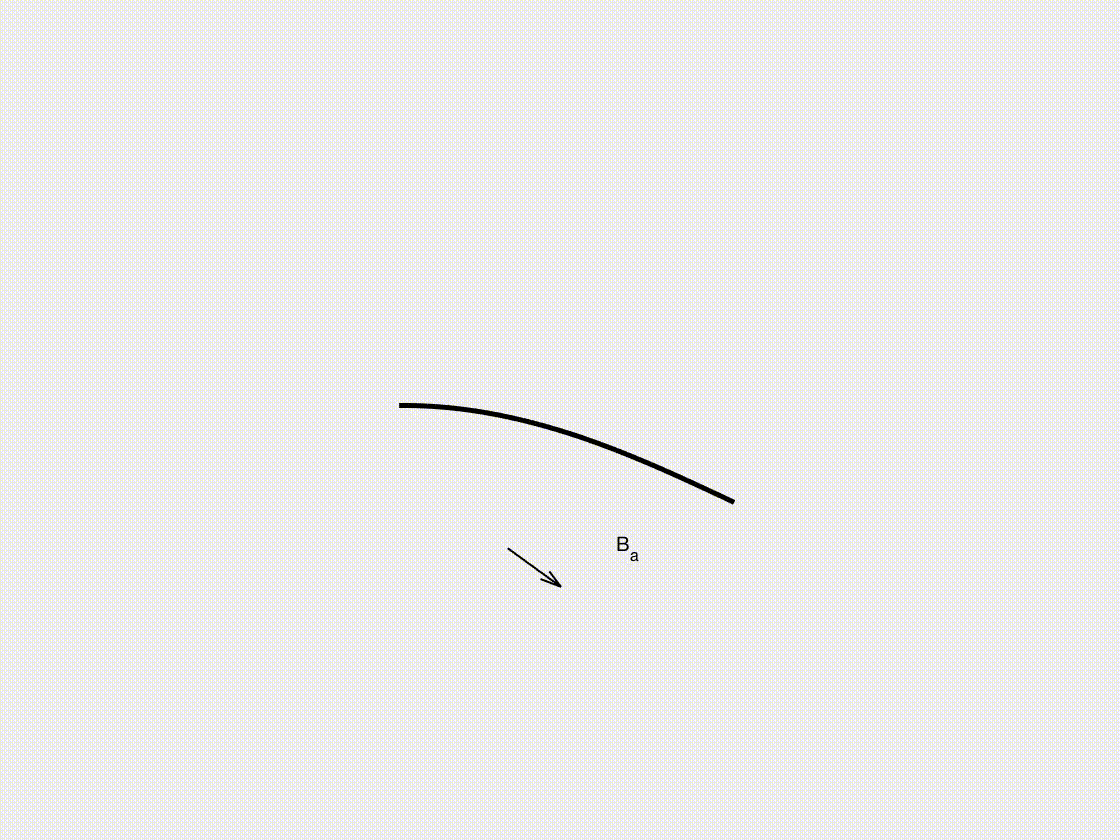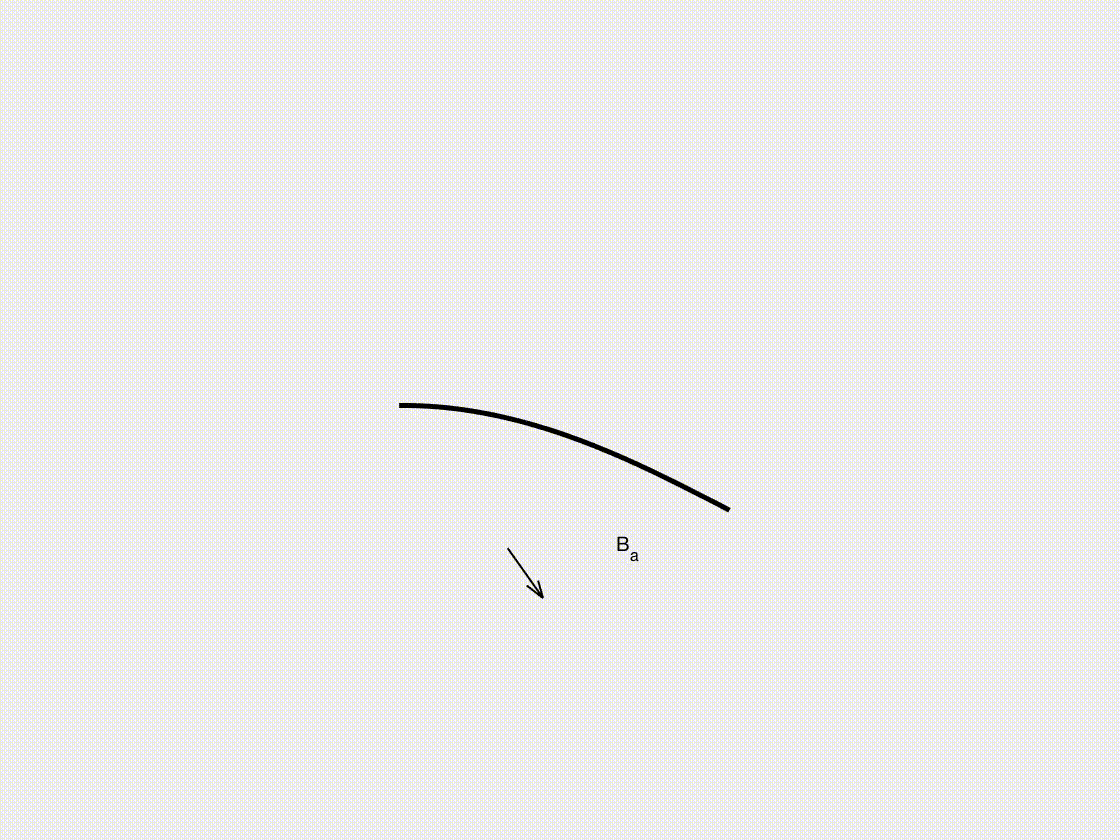
In this subsection, we illustrate the dynamic response of a magnetized beam subjected to external magnetic actuation. Using the DDG simulation framework, we analyze how the beam deforms and oscillates in response to time-varying magnetic fields. As magnetically actuated structures are widely explored in soft robotics, biomedical devices, and adaptive materials, this case highlights the potential of our approach in designing and optimizing magneto-mechanical systems for precise and controllable actuation.

Simulation Initialization

To initialize the simulation, the following inputs are used:

1. Geometry and connection:
   • (i) Nodal positions: the position of the nodes \(\mathbf{q}(t=0)\), with a total of \(N = 40\). The length of the magnetized beam is set at \(L = 1.0\mathrm{~m}\).
   • (ii) Stretching elements: the connections between the nodes, with a total of \(N_s = 39\).
   • (iii) Bending elements: the connections between the edges, with a total of \(N_b = 38\).
2. Physical parameters:
   • (i) Young’s modulus, \(E = 100\mathrm{~MPa}\).
   • (ii) Material density, \(\rho = 10.0\) \(\mathrm{kg/m^3}\).
   • (iii) Cross-sectional radius, \(r_0 = 0.01\mathrm{~m}\).
   • (iv) Damping viscosity, \(\mu = 0.1\).
   • (v) Gravitational field, \(\mathbf{g} = [0.0, 0.0]^T\) \(\mathrm{m/s^2}\).
   • (vi) The beam magnetization is \(\mathbf{B}_r = [1000.0, 0.0]\mathrm{~T/m^3}\).
   • (vii) The overall simulation is dynamic, i.e., \(\mathrm{ifStatic} = 0\).
3. Numerical parameters:
   • (i) Total simulation time, \(T = 20.0\mathrm{~s}\).
   • (ii) Time step size, \(\mathrm{dt} = 0.01\mathrm{~s}\).
   • (iii) Numerical force tolerance, \(\mathrm{tol} = 1 \times 10^{-4}\).
   • (iv) Maximum iterations, \(N_{\mathrm{iter}} = 10\).
4. Boundary conditions:
   • The left tip of the beam is clamped by fixing the first two nodes (starting from the left), thus the constrained index array is \(\mathcal{FIX} = [1, 2, 3, 4]^T\).
5. Initial conditions:
   • (i) Initial position is input from the nodal positions.
   • (ii) Initial velocity is set to zeros for all nodes.
6. Loading steps:
   • A magnetic field with \(B_x = A \cos(\omega t)\) and \(B_y = A \sin(\omega t)\) (where \(A = 3.0\mathrm{~T}\) and \(\omega = 1.0\mathrm{~rad/s}\)) is applied to the entire beam.

Dynamic Rendering