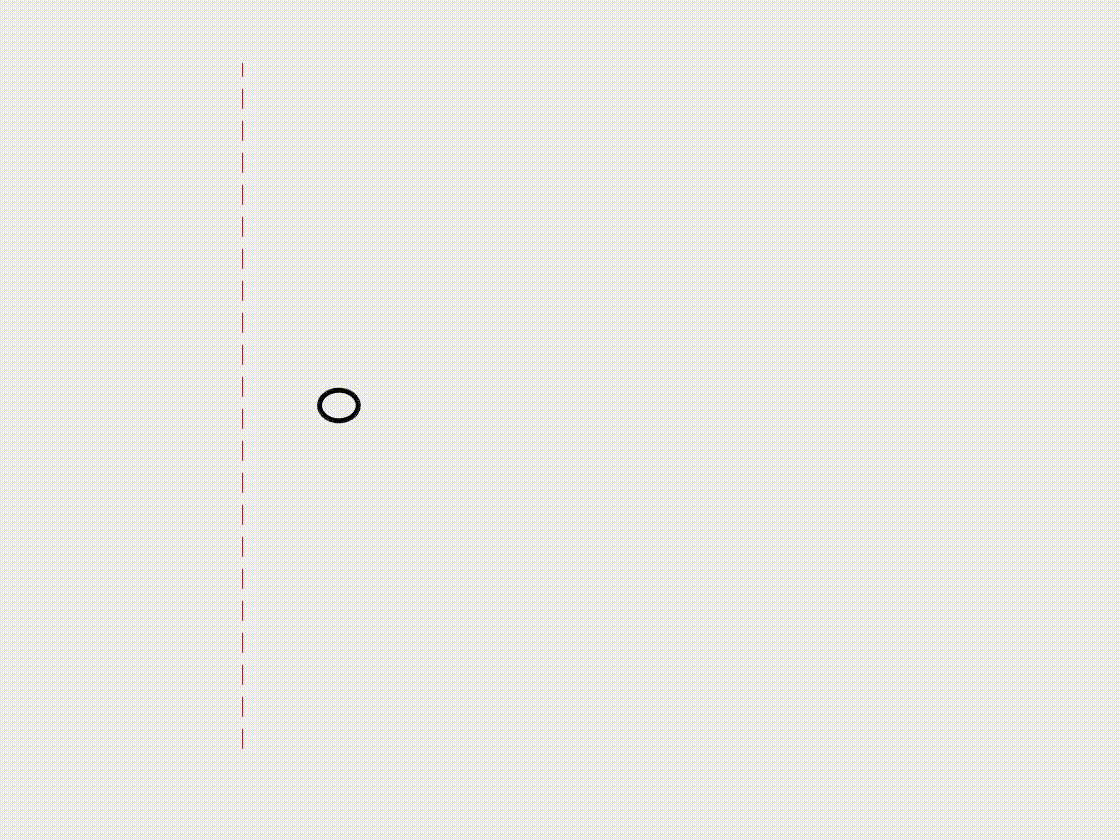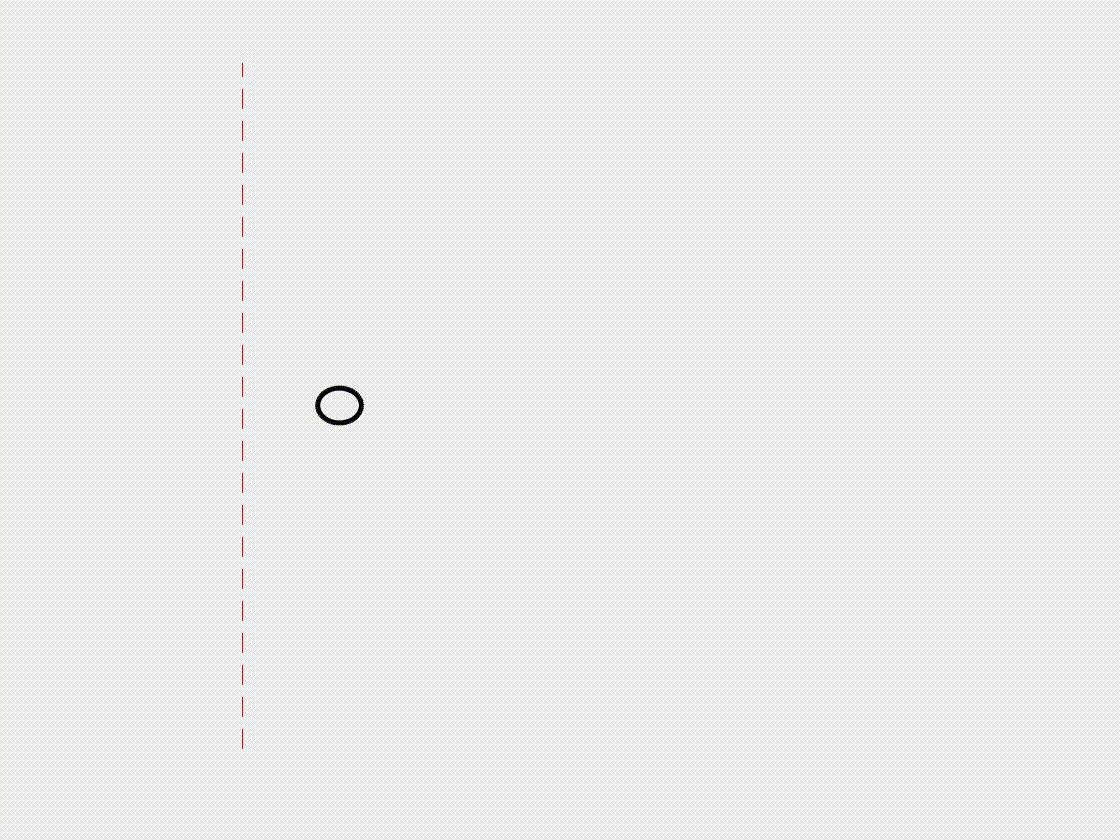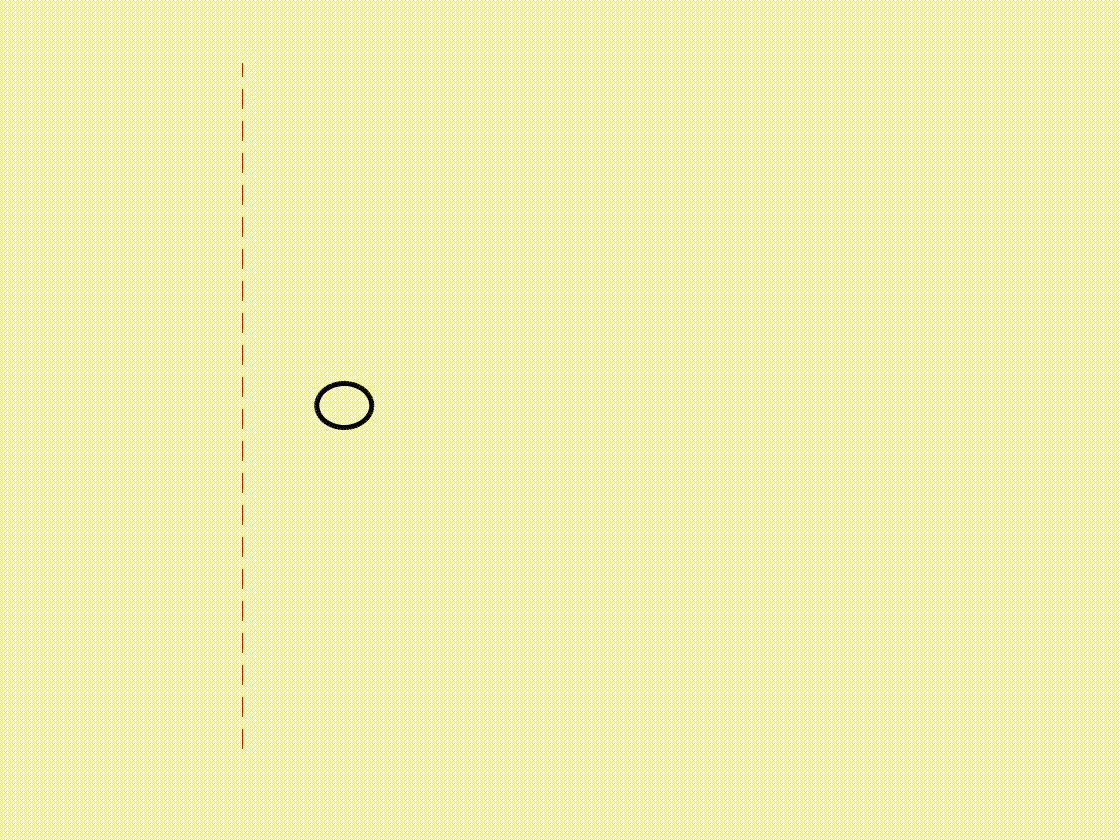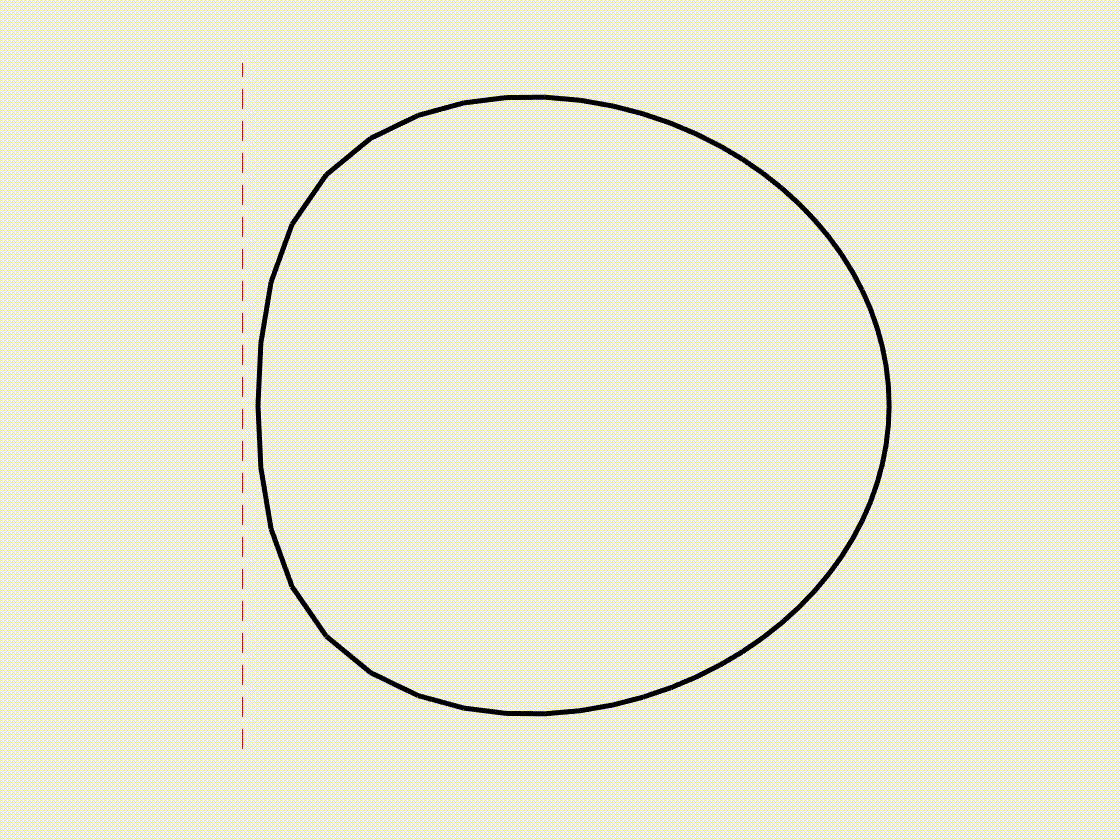
Hyperelastic axisymmetric membrane

In this subsection, we examine an axisymmetric membrane, a commonly used hyperelastic structure for soft actuators, to demonstrate the effectiveness of DDG in handling nonlinear hyperelastic constitutive laws. In contrast to the axisymmetric shell, where bending energy dominates, the axisymmetric membrane solely undergoes stretching, as seen in the inflation of a balloon. Moreover, due to the large physical strain, the linear elastic model fails to accurately describe the membrane’s inflation, making a hyperelastic model essential.

Simulation Initialization

To initialize the simulation, the following inputs are used:

1. Geometry and connection:
   • (i) Nodal positions: the position of the nodes \(\mathbf{q}(t=0)\), with a total of \(N = 60\). The radius of the circular cross-section \(R_1 = 0.2\) m. The outer radius, which is the distance from the center of the cross-section to the center of the torus, is \(R_2 = 1.0\) m.
   • (ii) Stretching elements: the connections between the nodes, with a total of \(N_s = 60\).
2. Physical parameters:
   • (i) Shear modulus, \(G = 0.333\mathrm{~MPa}\), thus \(C_1 = 0.4G\), and \(C_1 = 0.1G\).
   • (ii) Material density, \(\rho = 100.0\) \(\mathrm{kg/m^3}\).
   • (iii) Cross-sectional radius, \(r_0 = 0.01\mathrm{~m}\).
   • (iv) Damping viscosity, \(\mu = 1.0\).
   • (v) Gravity, \(\mathbf{g} = [0.0, 0.0]^T\mathrm{~m/s^2}\).
   • (vi) The overall simulation is dynamic, i.e., \(\mathrm{ifStatic} = 0\).
3. Numerical parameters:
   • (i) Total simulation time, \(T = 2.0\mathrm{~s}\).
   • (ii) Time step size, \(\mathrm{dt} = 0.01\mathrm{~s}\).
   • (iii) Numerical tolerance, \(\mathrm{tol} = 1 \times 10^{-4}\).
   • (iv) Maximum iterations, \(N_{\mathrm{iter}} = 10\).
4. Boundary conditions:
   • The \(Z\) direction of the first node is fixed to avoid rigid body motion, thus the constrained array, \(\mathcal{FIX} = [2]\).
5. Initial conditions:
   • (i) Initial position is input from the nodal positions.
   • (ii) Initial velocity is set to zeros.
6. Loading steps:
   • The external pressure load is increased at a rate \(\dot{p} = 10.0\mathrm{~kPa/s}\).

Dynamic Rendering