What is Discrete Differential Geometry (DDG)?

Discrete differential geometry (DDG) has emerged as a promising numerical framework for simulating flexible structures, particularly in scenarios involving large deformations, geometric complexity, and nonlinear interactions. Initially developed in the computational graphics and computer geometry communities, DDG has gained increasing recognition in structural mechanics for its ability to preserve geometric properties while efficiently modeling thin elastic structures, such as rods, ribbons, plates, and shells. Unlike conventional numerical methods, which focus on discretizing differential equations, DDG instead discretizes the underlying geometry itself, enabling more efficient and stable simulations of complex deformations.

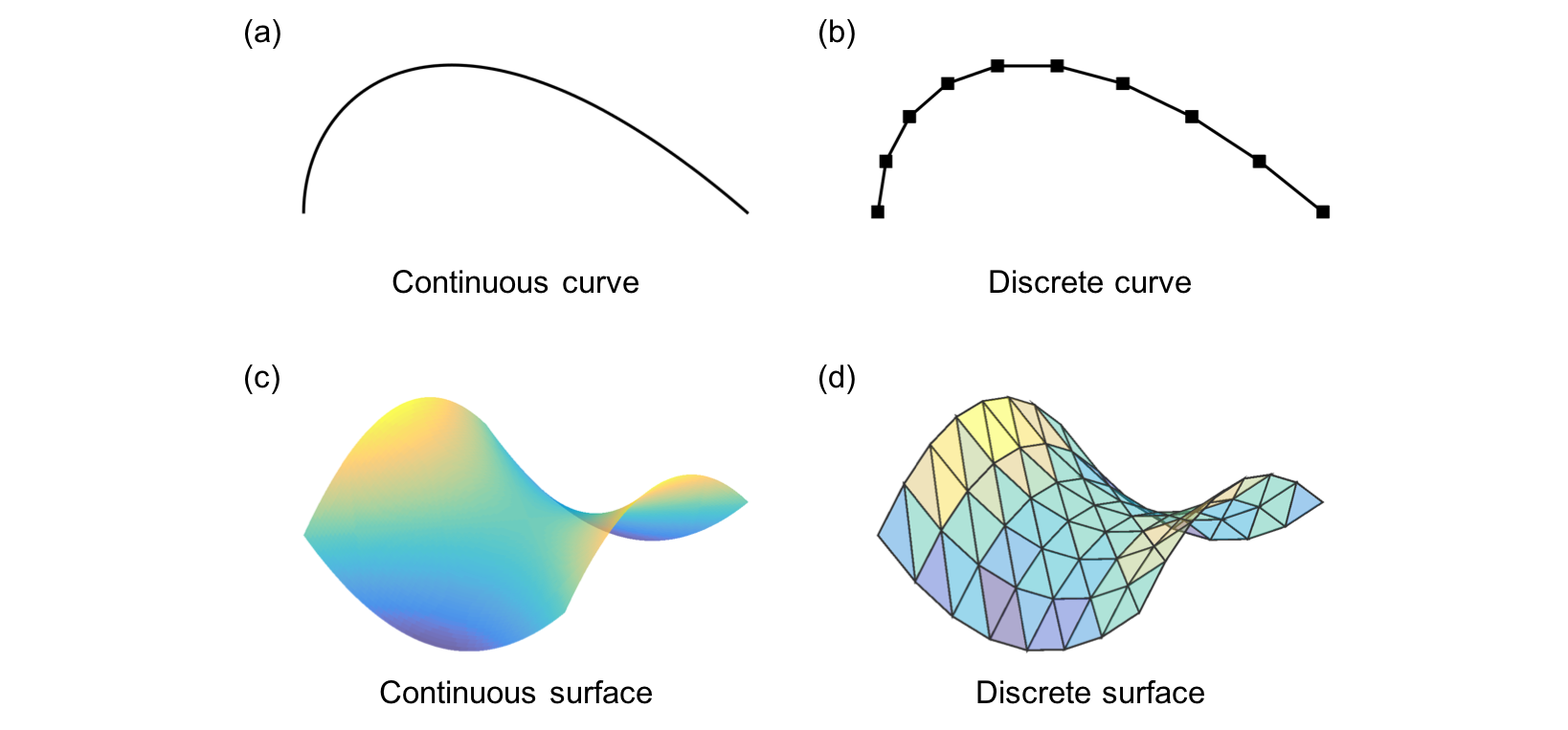Geometry discretizations in DDG simulations: (a-b) A continuous curve is approximated using discrete nodes and edges. (c-d). A continuous surface is approximated using discrete triangular elements.

Key Advantages of the DDG Method

• Intrinsic Geometric Preservation: DDG maintains curvature and topological constraints, making it particularly well-suited for thin and highly deformable structures.
• Robustness to Large Deformations: Unlike FEM, DDG avoids locking effects and accurately captures bending, twisting, and instability-driven deformations.
• Efficient Computation: DDG simplifies numerical integration, leading to faster and more stable simulations compared to traditional methods.
• Seamless Multi-Physics Integration: Interaction with external fields, such as magneto-elastic coupling, fluid-structure interactions, and contact with solids can be incorporated without compromising geometric consistency.

Application

• Biological Systems and Bio-Locomotion: Biological locomotion, fluid transport, and sensing rely on highly deformable structures like flagella and cilia, which interact with surrounding fluids through nonlinear bending mechanics. DDG effectively models these dynamics, supporting research on microorganism motility, mucus transport, and bio-inspired swimming robots.
• Soft Robots and Soft Actuators: Soft robots use flexible structures for adaptive movement, requiring models that simulate large deformations and dynamic interactions. DDG enables stable simulations for these robots, capturing interactions like contact mechanics and fluid coupling.
• Deployable and Morphing Structures: Deployable structures in aerospace, space exploration, and adaptive architecture rely on bistability and morphing materials for shape transitions. DDG efficiently models these mechanisms, capturing large-scale deformations while ensuring mechanical robustness and geometric fidelity.
• Mechanical Metamaterials and Programmable Structures: Mechanical metamaterials use geometric design to achieve tunable properties like negative Poisson’s ratios and bistability. DDG efficiently simulates these structures, aiding applications in adaptive actuators, biomedical implants, and energy-absorbing materials.
• Flexible Electronics and Bio-Integrated Devices: Flexible electronics and bio-integrated devices must withstand continuous deformation while maintaining functionality. DDG efficiently simulates thin-film deformations and strain effects, aiding the design of durable wearable and medical devices.

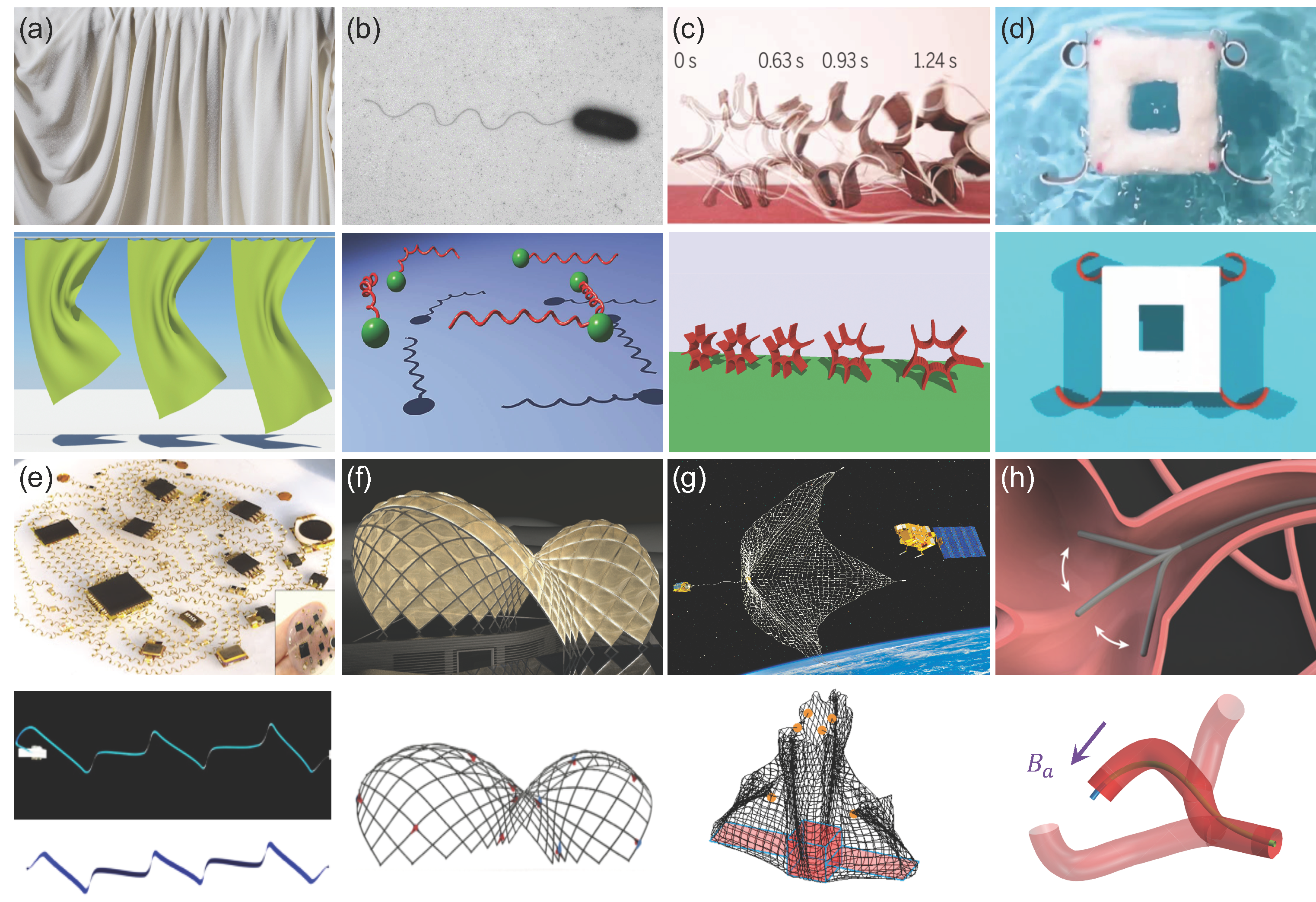Applications of DDG-based simulations: (a) Computer graphics. (b) Biophysics. (c) Soft robots. (d) Underwater robots. (e) Flexible electronics. (f) Civil engineering. (g) Aerospace engineering. (h) Biomedical engineering.

Objective of the Tutorial

Despite its advantages, the adoption of DDG in computational mechanics remains limited due to the lack of accessible resources and tutorials. This tutorial aims to bridge that gap by providing a comprehensive and practical guide to the use of DDG for nonlinear numerical simulation of flexible structures. This tutorial serves as a valuable resource for researchers and engineers working in computational mechanics, applied mathematics, structural design, and soft robotics.